PAS MATEMATIKA BLOG

Lanjutan Contoh Soal Persiapan untuk Numerasi AN BK 2022

$\LARGE\colorbox{yellow}{CONTOH SOAL 19}$.

Sebuah kolam berbentuk seperti gambar dengan panjang sampai ujung 10. Dua orang yang pada sebuah jalur lurus yang masing-masing berada pada posisi A dan B dan berjarak 8 kaki serta diketahui besar sudut sebagaimana ilustrasi pada gambar sebesar $60^{0}$. Tentukanlah jarak terpendek titik C ke jalur lurus tersebut

$\LARGE\colorbox{silver}{SOLUSI SOAL 19}$.

Jika kita sederhanakan gambar ilustrasi di atas adalah sebagai berikut

Kita akan menentukan panjang ruas garis yang berwarna merah di atas. Selanjutnya perhatikanlah

$\begin{aligned}&\textrm{Pada soal di atas, kita diminta untuk}\\ &\textrm{menentukan garis merah yang selanjutnya}\\ &\textrm{di sebut tinggi di sini}\\ &\color{red}\textrm{Dengan bantuan luas segitiga ABC}\\ &\textrm{kita mendapatkan}\\ &\begin{aligned}\left [ ABC \right ]&=\left [ ABC \right ]\\ \displaystyle \frac{\textrm{alas}\times \textrm{tinggi}}{2}&=\displaystyle \frac{1}{2}AB.BC\sin \angle B\\ \displaystyle \frac{\textrm{AB}\times \textrm{tinggi}}{2}&=\displaystyle \frac{1}{2}AB.BC\sin 60^{0}\\ \textrm{tinggi}&=BC\left ( \displaystyle \frac{1}{2}\sqrt{3} \right ) \end{aligned}\\ &\textrm{Dengan aturan cosinus kita juga akan}\\ &\textrm{dapatkan}\\ &\begin{aligned}AC^{2}&=AB^{2}+BC^{2}-2.AB.BC.\cos \angle B\\ 10^{2}&=8^{2}+BC^{2}-2.8.BC.\cos 60^{0}\\ 10^{2}&-8^{2}=BC^{2}-2.8.BC.\left ( \displaystyle \frac{1}{2} \right )\\ BC^{2}&-8BC-36=0\\ BC_{1,2}&=\displaystyle \frac{-(-8)\pm \sqrt{(-8)^{2}-4.(-36)}}{2}\\ &=\displaystyle \frac{8\pm \sqrt{64+144}}{2}=\displaystyle \frac{8\pm \sqrt{208}}{2}\\ &=\displaystyle \frac{8\pm 4\sqrt{13}}{2}=4\pm 2\sqrt{13}\\ &\color{purple}\textrm{pilih nilai BC yang positif, yaitu}\\ BC&=4+2\sqrt{13} \end{aligned}\\ &\textrm{Selanjutnya}\\ &\textrm{Tinggi}=\displaystyle \frac{1}{2}BC\sqrt{3}=\color{red}\displaystyle \frac{1}{2}\left ( 4+2\sqrt{13} \right )\sqrt{3}\:\textrm{ m} \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL 20}$.

Sebuah kolam renang akan dibangun di area tanah yang berbentuk segitiga. Selain kolam renang juga akan dibangun ruang ganti kecil (lihat gambar berikut)

Tentukan jari-jari maksimu kolam renang jika tepi kolam renang bersinggungan dengan ruang ganti

$\LARGE\colorbox{silver}{SOLUSI SOAL 20}$.

$\begin{aligned}&\textrm{Perhatikan bahwa}\\ &\begin{aligned}\left [ \textrm{ruang ganti} \right ]&=\textrm{luas ruang ganti, dengan}\\ s&=\displaystyle \frac{1}{2}(\color{red}a\color{black}+b+c)\Leftrightarrow s=\frac{4+5+6}{2}=\displaystyle \frac{15}{2}\\ \left [ \textrm{ruang ganti} \right ]&=\sqrt{s(s-\color{red}a\color{black})(s-b)(s-c)}\\ &=\sqrt{\displaystyle \frac{15}{2}\left (\frac{15}{2}-4 \right )\left ( \frac{15}{2}-5 \right )\left (\frac{15}{2}-6 \right )}\\ &=\sqrt{\frac{15}{2}.\frac{7}{2}.\frac{5}{2}.\frac{3}{2}}=\frac{15}{2}\sqrt{\frac{7}{2}.\frac{2}{2}}=\frac{15}{4}\sqrt{14}\\ \textrm{Selain rumus}&\: \textrm{di atas, rumus luas juga berupa}\\ \left [ \textrm{ruang ganti} \right ]&=r_{\color{red}a\color{black}}(s-\color{red}a\color{black})\\ \displaystyle \frac{15}{4}\sqrt{14}&=r_{\color{red}a\color{black}}.\displaystyle \frac{7}{2}\Leftrightarrow \displaystyle \frac{15}{14}\sqrt{14}=r_{\color{red}a\color{black}} \end{aligned}\\ &\textrm{Jadi, jari-jarinya adalah}\: \: \color{red}\displaystyle \frac{15}{14}\sqrt{14}\: \: \color{black}\textrm{m} \end{aligned}$.

DAFTAR PUSTAKA

Tampomas, H. 1999. SeribuPena Matematika SMU Jilid 1 Kelas 1. Jakarta: ERLANGGA.

Contoh Soal Persiapan untuk Numerasi AN BK 2022

Konsep Materi dan Contoh dan Pembahasan Numerasi Soal no. 1 - 5
Contoh Soal dan Pembahasan Numerasi no. 6 - 10
Contoh Soal dan Pembahasan Numerasi no. 11 - 12
Contoh Soal dan Pembahasan Numerasi no. 13
Contoh Soal dan Pembahasan Numerasi no. 14 - 15

$\LARGE\colorbox{yellow}{CONTOH SOAL 16}$.

(Di adaptasi dari soal OSN Matematika SD 2008)

Perhatikanlah Kertas yang diberi garis lurus berikut

dengan menggambar sebuah garis lurus akan didapatkan dua daerah (lihat gambar 1 di atas)
dengan menggambar dua garis lurus akan didapatkan paling banyak empat daerah (lihat gambar 2 di atas)
dengan menggambar tiga garis lurus akan didapatkan paling banyak tujuh daerah (lihat gambar 3 di atas)

(a) Dengan menggambar empat garis lurus, berapa daerah paling banyak akan didapatkan?

(b) Dengan menggambar tujuh garis lurus, berapa daerah paling banyak akan didapatkan?

$\LARGE\colorbox{silver}{SOLUSI SOAL 16}$.

$\begin{aligned}&\color{blue}\textbf{Alternatif 1}\\ &\begin{array}{|l|c|c|c|c|c|}\hline \textrm{Banyak garis}&0&1&2&3&4\\\hline \textrm{Maksimum daerah}&1&2&4&7&11\\\hline &&\begin{matrix} \downarrow\\ U_{1} \end{matrix}&\begin{matrix} \downarrow\\ U_{2} \end{matrix}&\begin{matrix} \downarrow\\ U_{3} \end{matrix}&\begin{matrix} \downarrow\\ U_{4} \end{matrix}\\\hline \end{array}\\ &\textbf{Polanya adalah}\\ &\qquad\qquad\begin{aligned}&\underset{2}{\underbrace{\begin{matrix} 2 & 4 \end{matrix}}}\underset{3}{\underbrace{\begin{matrix} & 7 \end{matrix}}}\underset{4}{\underbrace{\begin{matrix} & 11 \end{matrix}}}\underset{\cdots }{\underbrace{\begin{matrix} & \cdots \end{matrix}}} \end{aligned}\\ &\textrm{Merupakan barisan aritmetika tingkat dua}\\ & \end{aligned}$.

Silahkan gunakan cara penyelesaian yang kurang lebih sama dengan yang di sini.

maka akan didapatkan rumus $U_{n}=\displaystyle \frac{n(n+1)}{2}+1$.

$\begin{aligned}(\textrm{a}).\quad&n=4\rightarrow U_{4}=\color{red}11\\ (\textrm{b}).\quad&n=7\rightarrow U_{7}=\displaystyle \frac{7\times 8}{2}+1=\color{red}29\\ (\textrm{c}).\quad&n=20\rightarrow U_{20}=\displaystyle \frac{20\times 21}{2}+1=\color{red}211\\ \end{aligned}$.

$\begin{aligned}&\color{blue}\textbf{Alternatif 2}\\ &\textrm{Untuk Barisan dengan selisih tetap atau}\\ &\textrm{lebih dikenal dengan barisan aritmetika secar}\\ &\textrm{umum dapat dituliskan untuk suku}\: \: \textrm{ke}-n\\ &U_{n}=U_{1}+\begin{pmatrix} n-1\\ 1 \end{pmatrix}b_{1}^{1}+\begin{pmatrix} n-1\\ 2 \end{pmatrix}b_{1}^{2}+\cdots +\begin{pmatrix} n-1\\ k \end{pmatrix}b_{1}^{k}\\ &\textrm{dengan}\quad U_{1}=\textrm{suku pertama}\rightarrow U_{1}=2\\ &\qquad\qquad b_{1}^{1}=\textrm{selisih tingkat 1}\rightarrow b_{1}^{1}=4-2=2\\ &\qquad\qquad b_{1}^{2}=\textrm{selisih tingkat 2}\rightarrow b_{1}^{2}=1\\ &\textrm{Untuk tingkat 2},\\ &\begin{aligned}U_{n}&=U_{1}++\begin{pmatrix} n-1\\ 1 \end{pmatrix}b_{1}^{1}+\begin{pmatrix} n-1\\ 2 \end{pmatrix}b_{1}^{2}\\ &=U_{1}+(n-1)b_{1}^{1}+\displaystyle \frac{(n-1)(n-2)}{2}b_{1}^{2}\\ &=2+(n-1)(2)+\displaystyle \frac{(n-1)(n-2)}{2}(1)\\ &=2+2n-2+\displaystyle \frac{(n-1)(n-2)}{2}\\ &=2n+\displaystyle \frac{n^{2}-3n+2}{2}\\ &=\displaystyle \frac{n^{2}+n+2}{2}=\displaystyle \frac{n^{2}+n}{2}+1\\ U_{n}&=\color{red}\displaystyle \frac{n(n+1)}{2}+1\color{black},\: \textrm{maka}\\ U_{4}&=\displaystyle \frac{4.5}{2}+1=\color{red}11\\ U_{7}&=\displaystyle \frac{7.8}{2}+1=\color{red}29\color{black},\: \: \textrm{serta}\\ U_{20}&=\displaystyle \frac{20.21}{2}+1=\color{red}211 \end{aligned} \end{aligned}$.

Diberikan teks berikut untuk soal 17 dan 18

$\LARGE\colorbox{yellow}{CONTOH SOAL 17}$.

(Di adaptasi dari soal UMPTN 1997 IPA Terpadu)

KESEIMBANGAN ENERGI PADA DAUN

Laju fotosintesis total F didefinisikan sebagai jumlah total karbohidrat yang terbentuk dalam proses fotosintesis persatuan waktu. Hasil fotosintesis neto N didefinisikan sebagai sisa karbohidrat persatuan waktu setelah respirasi memecah karbohidrat sejumlah R persatuan waktu. Kelakuan besaran-besaran tersebut terhadap suhu antara $10^{0}$ C sampai $30^{0}$ C diamati sebagaimana berikut ini.

Ketika suhu naik, F bertambah lebih cepat dari pada R (yang naik secara eksponensial), tetapi segera mencapai harga yang tetap karena keterbatasan $CO_{2}$, sehingga N mulai menurun. Jadi N terhadap suhu hampir berbentuk parabola dengan puncak sekitar $18^{0}$ C.

Suhu daun dikendalikan oleh energi yang datang dan energi yang dikeluarkan. Energi dikeluarkan dari daun melalui proses konduksi ke sekelilingnya, dengan radiasi gelombang panjang, dan melalui transpirasi yang dapat berkisar antara 25% hingga 50%.

Bila pori daunnya tertutup untuk menahan penguapan air, maka suhunya naik. Radiasi terutama terjadi pada malam hari ketika tidak berawan sehingga daunnya mendingin.

$\begin{array}{ll}\\ &\textrm{Jika jumlah N pada suhu}\: \: 10^{0}C\: \textrm{adalah a dan}\\ &\textrm{pada suhu}\: 30^{0}C\: \textrm{adalah b, maka N pada suhu t}\\ &\textrm{sekitar}\\ &(\textrm{a})\quad \displaystyle \frac{b-a}{80}t^{2}-\displaystyle \frac{9b-9a}{20}t+\displaystyle \frac{13b-9a}{4}\\ &(\textrm{b})\quad \displaystyle \frac{b-a}{80}t^{2}+\displaystyle \frac{9b-9a}{20}t+\displaystyle \frac{13b-9a}{4}\\ &(\textrm{c})\quad \displaystyle \frac{a-b}{80}t^{2}-\displaystyle \frac{9b-9a}{20}t+\displaystyle \frac{13b-9a}{4}\\ &(\textrm{d})\quad \displaystyle \frac{a-b}{80}t^{2}+\displaystyle \frac{9b-9a}{20}t+\displaystyle \frac{13b-9a}{4}\\ &(\textrm{e})\quad \displaystyle \frac{b-a}{80}t^{2}-\displaystyle \frac{9b-9a}{20}t-\displaystyle \frac{13b-9a}{4}\\ \end{array}$.

$\LARGE\colorbox{silver}{PEMBAHASAN SOAL NO.17}$.

$\begin{aligned}&\textrm{Diketahui fungsi berbentuk parabola dengan}\\ &f(t)=pt^{2}+qt+r.\: \: \textrm{Selanjutnya}\\ &\begin{array}{llllr} &f(t)&=\color{red}pt^{2}+qt+r\\ &f(10)&=100p+10q+r&=a\: \: .......(1)\\ &f(30)&=900p+30q+r&=b\: \: .......(2)&-\\\hline &&-800p-20q&=a-b \end{array}\\ &\textrm{dan puncaknya di}\: \: t_{puncak}=-\displaystyle \frac{q}{2p}=18,\\ &\Leftrightarrow q=-36p\: \: ............(4)\\ &\textrm{Dari persamaan}\: (3)\: \&\: (4)\\ &-800p-20q=a-b\\ &\Leftrightarrow -800p-20(-36p)=a-b\\ &\Leftrightarrow -800p-720q=a-b\\ &\Leftrightarrow -80p=a-b\\ &\Leftrightarrow p=\displaystyle \frac{b-a}{80},\: \: \textrm{maka}\: \: q=\displaystyle \frac{-9b+9a}{20}\\ &\: \quad\textrm{dan}\: \: r=\displaystyle \frac{13b-9a}{4}\\ &\textrm{Sehingga}\\ &f(t)=\color{red}\displaystyle \frac{b-a}{80}t^{2}-\displaystyle \frac{9b-9a}{20}t+\frac{13b-9a}{4} \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL 18}$.

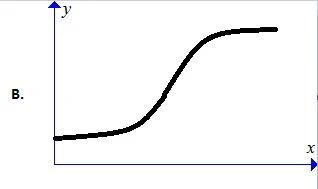
$\begin{array}{ll} \textrm{Grafik F di atas terhadap suhu berbentuk seperti} \end{array}$.

$\LARGE\colorbox{silver}{SOLUSI SOAL 18}$.

Cukup Jelas opsi yang tepat adalah C

DAFTAR PUSTAKA

Departemen Operasi Lembaga Pendidikan Primagama. 1997. Siap UMPTN Kelompok IPA. Yogyakarta: PT. Mitra Prima Media.
Sobel, M. A., Maletsky, E.M. 2004. Mengajar Matematika Sebuah Buku Sumber Alat Peraga, Aktivitas, dan Strategi untuk Guru Matematika SD, SMP, SMA. Jakarta: ERLANGGA.
Wibowo, S.S. 2015. Kumpulan Soal & Pembahasan Olimpiade Matematika SD Jilid 1. Bandung: YRAMA WIDYA.

Lanjutan Materi Elips

Elips

A. Definisi

Definisi 1

Elips adalah tempat kedudukan titik-titik di mana jumlah jaraknya terhadap dua titik tertentu selalu sama.

Perhatikan ilustrasi berikut

Misalkan $\color{red}F_{1}$ dan $\color{red}F_{2}$ masing-masing adalah fokus dari elips sebagaimana ilustrasi gambar di atas dengan $\color{red}F_{1}F_{2}=2c$ dan misalkan juga jumlah jarak suatu titik pada elips ke $\color{red}F_{1}$ dan $\color{red}F_{2}$ sama dengan $2a$ ($\color{red}2a$ tetap dan $\color{red}2a>2c>0$)

Ilustrasi bantu dengan lingkaran

Buatlah lingkaran dengan pusat di $\color{red}F_{1}$ dengan $\color{red}r_{1}=a-c$ dan lingkaran kedua dengan pusat di $\color{red}F_{2}$ dengan $\color{red}r_{1}=a+c$ (atau diblaok balik), maka lingkaran di $\color{red}F_{2}$ akan memotong lingkaran di di $\color{red}F_{1}$ pada titik-titik yang yang memenuhi definisi elips tersebut di atas.

$\begin{aligned}&\textrm{Misalkan}\: \: F_{1}F_{2}=2c=6\: \: (c=3)\\ &\qquad\qquad\textrm{dan}\: \: 2a=8\: \: (a=4)\\ &\textrm{Dengan}\\ &a-c=4-3=1\: \: \textrm{dan}\: \: a+c=4+3=7\\ &\textrm{Sehingga}\\ &\begin{array}{|c||c|c|c|c|c|c|c|}\hline \color{red}r_{1}&1&2&3&4&5&6&7\\\hline \color{red}r_{2}&7&6&5&4&3&2&1\\\hline \end{array} \end{aligned}$.

Hal-hal yang berkaitan dengan elips.

$\begin{array}{|l|c|c|}\hline \color{red}\textrm{Sumbu Simetri (Sb)}&\textrm{Sb. Utama}&\textrm{Sb. Sekawan}\\ &A_{1}A_{2}&B_{1}B_{2}\\\hline \color{red}\textrm{Titik Pusat}&O&O\\\hline \color{red}\textrm{Latus rectum}&\begin{aligned}&\textrm{Garis melalui}\\ &F_{1}\: \: \textrm{dan tegak}\\ &\textrm{lurus sumbu}\\ &\textrm{utama, yaitu}\\ &L_{1}L_{1}' \end{aligned}&\begin{aligned}&\textrm{Garis melalui}\\ &F_{2}\: \: \textrm{dan tegak}\\ &\textrm{lurus sumbu}\\ &\textrm{utama, yaitu}\\ &L_{2}L_{2}' \end{aligned}\\\hline \color{red}\textrm{Keterkaitan}\: \color{black}a,b,c&\begin{aligned}&a^{2}=b^{2}+c^{2} \end{aligned}&a^{2}=b^{2}+c^{2}\\\hline \end{array}$.

Sebagai catatan pada elips ada dua sumbu simetri, yaitu sumbu utama dan sumbu sekawan. Sumbu utama juga disebut sebagai sumbu mayor atau sumbu panjang atau sumbu transversal dan sumbu ini berpotongan dengan elips di titik $\color{red}A_{1}$ dan $\color{red}A_{2}$ yang selanjutnya masing-masing disebut sebagai pucak dari elips tersebut. Adapun sumbu yang satunya adalah sumbu sekawan atau sumbu minor atau sumbu pendek atau sumbu konjungsi yaitu sumbu simetri yang melalui titik tengah $\color{red}F_{1}F_{2}$ dan tegak lurus dengan $\color{red}F_{1}F_{2}$ serta sumbu ini berpotongan dengan elips di titik $\color{red}B_{1}$ dan $\color{red}B_{2}$.

Definisi 2

Elips adalah kedudukan titik-titik yang perbandingan jaraknya ke titik tertentu...

B. Persamaan Elips

B. 1 Persamaan Elips berpusat di O(0,0)

$\LARGE\begin{array}{|c|}\hline \begin{aligned}&\color{red}\displaystyle \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\\ &\qquad\textrm{atau}\\ &\color{red}b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2} \end{aligned} \\\hline \end{array}$.

Perhatikan gambar pertama di atas

$\begin{aligned}&PF_{1}+PF_{2}=2a\\ &\Leftrightarrow \sqrt{(x-c)^{2}+y^{2}}+\sqrt{(x+c)^{2}+y^{2}}=2a\\ &\Leftrightarrow \sqrt{(x-c)^{2}+y^{2}}=2a-\sqrt{(x+c)^{2}+y^{2}}\\ &\Leftrightarrow (x-c)^{2}+y^{2}=4a^{2}-4a\sqrt{(x+c)^{2}+y^{2}}\\ &\qquad\qquad\qquad\qquad\qquad\qquad +(x+c)^{2}+y^{2}\\ &\Leftrightarrow x^{2}-2cx+y^{2}=4a^{2}-4a\sqrt{(x+c)^{2}+y^{2}}\\ &\qquad\qquad\qquad\qquad\qquad\quad +x^{2}+2cx+y^{2}\\ &\Leftrightarrow 4a\sqrt{(x+c)^{2}+y^{2}}=4a^{2}+4cx\\ &\Leftrightarrow a\sqrt{(x+c)^{2}+y^{2}}=a^{2}+cx\\ &\Leftrightarrow a^{2}((x+c)^{2}+y^{2})=a^{4}+2a^{2}cx+c^{2}x^{2}\\ &\Leftrightarrow a^{2}x^{2}+2a^{2}cx+a^{2}c^{2}+a^{2}y^{2}=a^{4}+2a^{2}cx+c^{2}x^{2}\\ &\Leftrightarrow (a^{2}-c^{2})x^{2}+a^{2}y^{2}=a^{2}(a^{2}-c^{2})\\ &\Leftrightarrow \color{red}b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2}\\ &\Leftrightarrow \color{red}\displaystyle \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 \end{aligned}$.

Eksentrisitas dan Persamaan direktris

Perhatikan ilustrasi berikut